Effect Size

The magnitude of difference between two groups

Authors

Affiliations

Nate Yomogida, B.S., SPT

Doctor of Physical Therapy

B.S. in Kinesiology

Chloë Kerstein, B.S., SPT

Doctor of Physical Therapy

B.A. in Neuroscience

Overview

• Effect size is a measure of the difference between sample means¹.
• Effect size could be considered “How much something changes after a specific intervention”¹.
• Effect size measures the extent to which two samples do not overlap¹.
• Often Abbreviated “d” (Cohen’s d)

Types of Effect Size

Raw Score Effect Size

Raw score effect size provides the literal mean difference between mean group scores¹.

Symbol	Meaning
\(\mu_1\)	Sample 1 mean1
\(\mu_2\)	Sample 2 mean1

\[ \textrm{Raw Score Effect Size} = \mu_1 - \mu_2 \]

Standardized Effect Size

The standardized effect size is the raw score effect size divided by the standard deviation of its respective population¹.

Symbol	Meaning
d	Cohen’s D (Effect Size)1
\(\mu_1\)	Sample 1 mean1
\(\mu_2\)	Sample 2 mean1
\(\sigma\)	Standard Deviation of the Population

\[ \textrm{d} = \frac{\mu_1 - \mu_2}{\sigma} \]

Standardized Effect size allows one to compare effect sizes between different measures. For example, standardized effect size allows a researcher to compare a pain scale from 0-43 to another pain scale which ranges from 0-10¹.

Note

• Notice that you are using standard deviation of the population (σ) not standard deviation of the distribution of means (\(\sigma_M\))¹
• In addition you are only concerned with one population’s standard deviation¹.
• In hypothesis testing, all of your participants should be from the same overall population¹.

Example

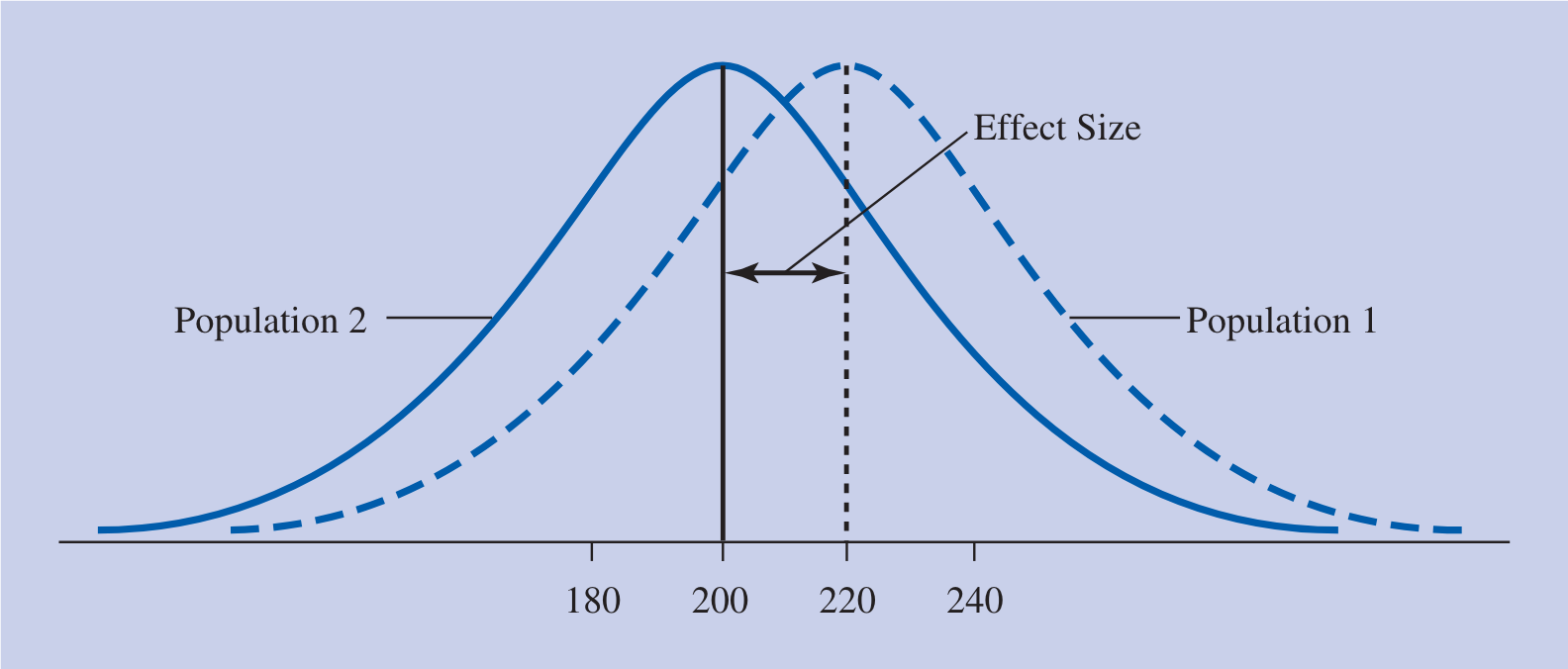
Experiment A results:

• Control group mean: 200
• Experimental group mean: 220
• Raw Score Effect size: \(220-200=\textbf{20}\)
• Standardized Effect size: \(\textrm{d} = \frac{\mu_1 - \mu_2}{\sigma} =\frac{220-200}{48} = \textbf{0.416}\)

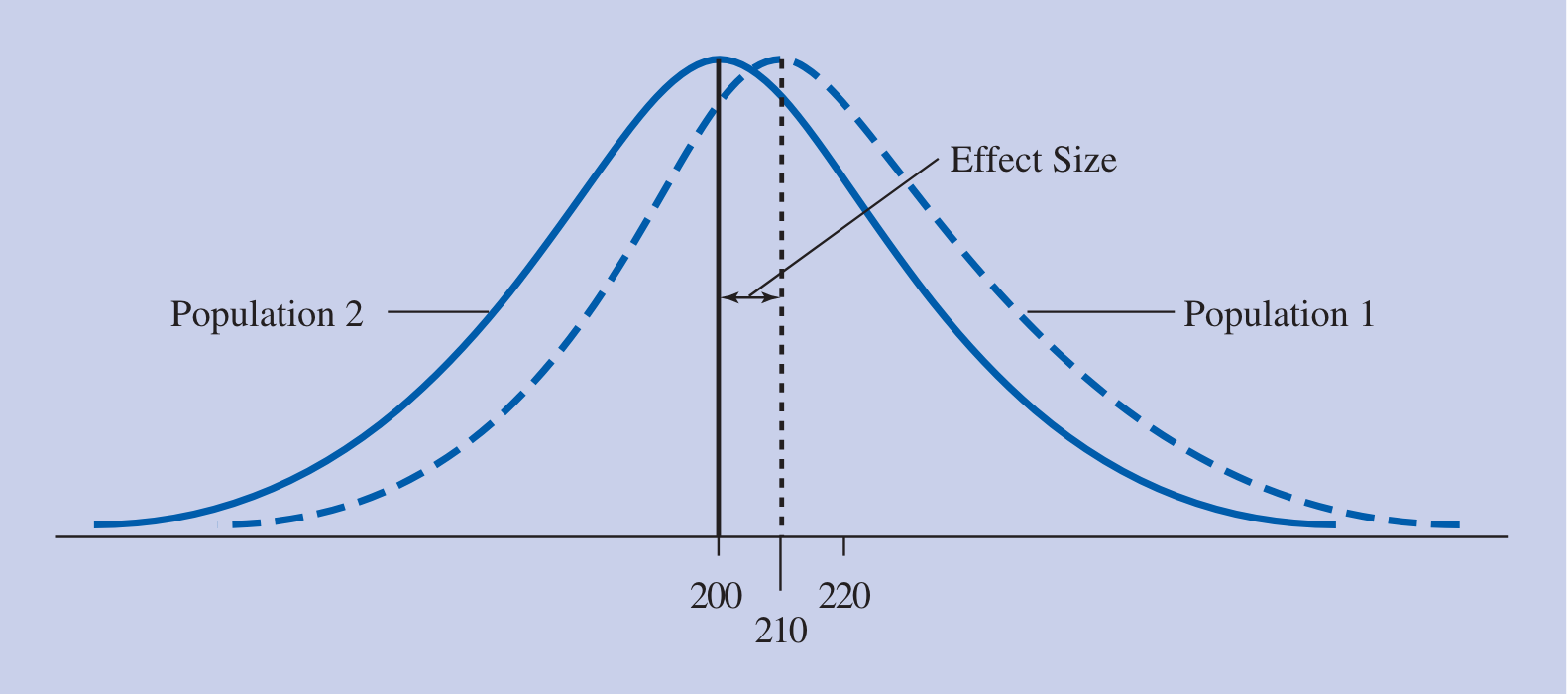
Experiment B Results

• Control group mean: 200
• Experimental group mean: 210
• Raw Score Effect size: \(210-200=\textbf{10}\)
• Standardized Effect size: \(\textrm{d} = \frac{\mu_1 - \mu_2}{\sigma} = \frac{210-200}{48} = \textbf{0.208}\)

Experiment A Effect size compares the means of the control group (200) with the experimental group (220)

Experiment B Effect size compares the means of the control group (200) with the experimental group (210)

When comparing these two experiments, we can visually see that Experiment A has a much larger effect size.

References

1.

Aron A, Coups EJ, Aron E. Statistics for Psychology. 6th ed. Pearson; 2013.